ML-Sharing (Ep 1): Introduction to the Clustering Problem for Beginners & Non-Experts
29/8/2024 By Daves Tran
This post is a translation of ML-Sharing that I have originally written in Vietnamese, if you want to read this blog in Vietnamese you can find it in here
ML-Sharing (Ep 1): Vietnamese Version
Some opening before we jump in:
For anyone venturing into Machine Learning problems, you’ve likely encountered the “Unsupervised Learning (UL)” problem, and one of the issues explored in UL is data clustering. In this discussion, let's explore:
What is clustering, and why do we have clustering problems?
What are the methods to solve clustering problems?
What should be noted when solving a clustering problem?
# Note: This article is a general overview of the clustering problem and the basic ideas of the algorithms. It won’t delve into detailed coding implementations of each algorithm (I might discuss this more in the future 👋).
1. What’s Clustering & Why Does It Exist !
Before discussing clustering, let’s take a brief look at Unsupervised Learning!
Unsupervised Learning (UL) is a subset of Machine Learning (ML).
Machine Learning is a field focused on designing computer systems capable of decision-making similar to humans—through training on large datasets.
The unsupervised nature of UL is reflected in the type of data fed into the system (models). These data, in a typical context, have no inherent meaning (they don’t follow any rules or context). The computer’s task is to:
“Please make sense of this meaningless data by imposing some context or order to them.”
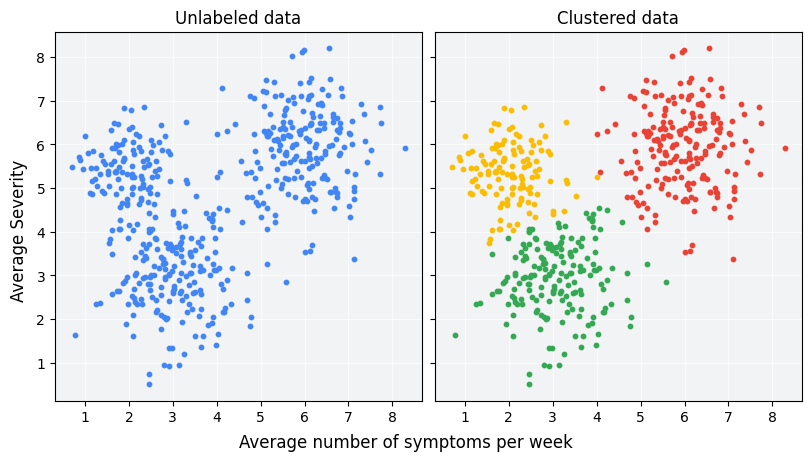
Returning to the clustering problem: in the context of clustering, your input is a set of random points (coordinates) with no particular pattern. Your model must find some relationship between these points and group them into clusters (the easiest relationship is through the distance between points).
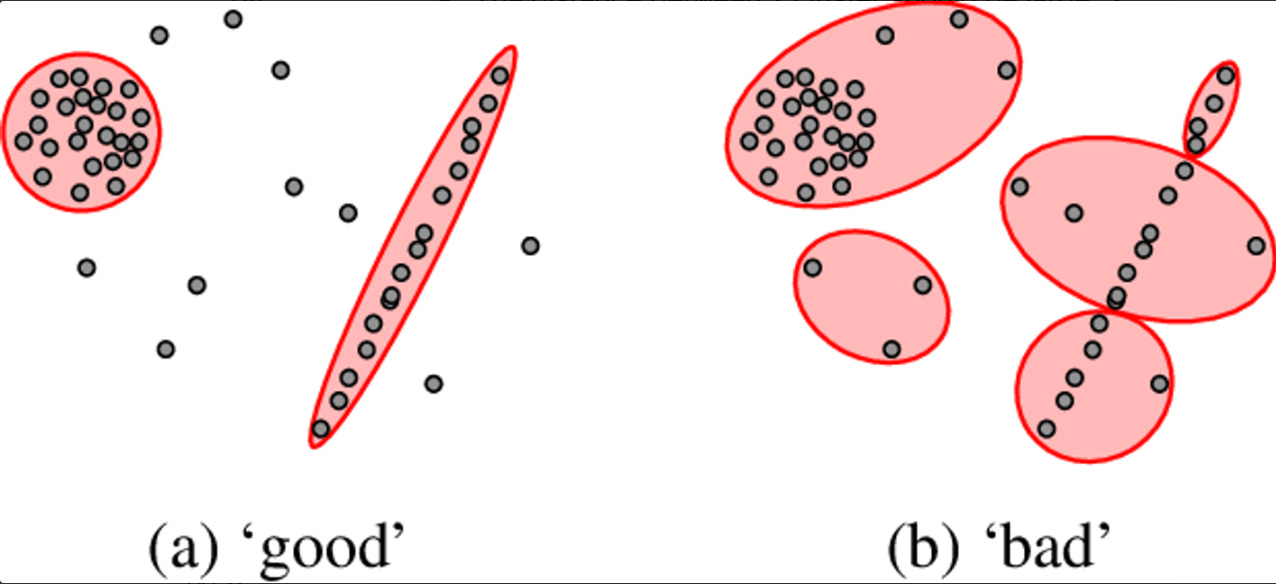
How do you know if your clustering solution is optimal and “acceptable”? One of the simplest methods is to visually observe the clustering results.
Your solution is ideal when, in the resulting space, the system produces n clusters where most or all points in each cluster are close together (no two points are too far apart). However, the distance between any two clusters should be significant (there should be a gap, as illustrated).
So, why does the clustering problem exist?
In my view, the data we collect from the environment often exists freely and chaotically. However, the process of decision-making (the pure idea of ML) requires the information to be logical, connected, and organized.
Besides making it easier to find ideas and information if everything is organized neatly, your machine system will also perform calculations more easily and won’t need to use too many resources to process the data.
Moreover, for large datasets, clustering can reduce storage capacity, while maintaining or even improving the effectiveness and quality of the ML process (accuracy, system memory).
2. What Are the Methods to Solve Clustering Problems?
There are several approaches to clustering problems, but two of the most basic methods include:
K-means (based on selecting K centroids on the plane of all data points).
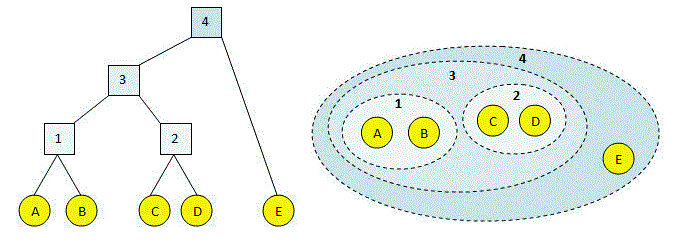
Hierarchical Clustering (the clustering relationships between data points can be divided into multiple hierarchical levels in a recursive manner—the result is a dendrogram structure).

K-means Algorithm:
The intuition of the algorithm:
Step 1: Choose K random centroids (the centroid is the average of the neighboring data points).
Step 2: Calculate the distance between each centroid and the small data points (instance data-points). For each instance data-point, choose the cluster by considering the distance to the nearest centroid.
Step 3: Continuously repeat steps 1 and 2 until the stopping condition is met (either a certain number of iterations or the movement of centroids becomes negligible—considered as reaching the optimal position).
Hierarchical Clustering Algorithm:
The intuition of the algorithm:
Step 1: Initially, have a dataset A with n data points—consider each data point as a small cluster with one element.
Step 2: Pair each small cluster (size = 1 point) with the nearest cluster to create a larger cluster B.
Step 3: Consider clusters B as single points (clusters with size = 1 point) and continue pairing with at least one individual data point or another adjacent cluster B’.
Generally, there are several ways to consider the distance between two clusters:
The nearest point (Simple linkage).
The farthest point (Complete linkage).
The centers of the two clusters compared to each other (Average linkage).
Step 4: Continuously repeat steps 1, 2, and 3 until all clusters merge into one cluster.

3. What Should We Note When Solving a Clustering Problem ? (*)
When solving any problem, we must all pay attention to the requirements and conditions of the question to provide the most accurate and effective solution—and in this case, the clustering problem also has several such requirements:
Requirement 1: Small Choice - Big Impact
In situations where you use a large dataset, you should also consider the distribution of the data—whether you want the data to be distributed according to a Gaussian Distribution (Normal distribution) or Exponent (exponential function). In other words, how do you want your data to be clustered or spread out?
The type of method you use to evaluate should also be considered—which method to use (in calculating the distance between two centroids or between two points), there are more than one calculation method, and each way will consume different computational resources. The choice of metric is also very important.
Deciding when to stop the algorithm - the clustering process: Knowing when to stop with the right number of clusters is essential (this applies when determining the K value in K-means and the stopping point in hierarchical clustering—before all points are merged into one cluster).
Requirement 2: Verify the Clusters Obtained from the Training Process:
Sometimes, your dataset may contain noise or outliers (extreme, rare cases in the sample).
Clustering algorithms are very sensitive to errors in data or outliers—results may not be optimal and could be unusable in solving larger problems with new datasets in the same context.
Requirement 3: How Users Interpret the Results of the Algorithm:
The results of any problem solved using ML applications often need to consider many issues related to ethics and transparency, and the clustering problem is no different.
Users (including data analysts or scientists) should consider using and reporting model results. Instead of presenting them as definitive facts, using them as hypotheses or statistical tools to support research processes will be a safer and fairer option.
(*) All the idea in the third section was come from:
James, G., Witten, D., Hastie, T., Tibshirani, R., & Taylor, J. (2023). An Introduction to Statistical Learning. In Springer texts in statistics (pp. 533–535). Springer. https://doi.org/10.1007/978-3-031-38747-0
Final Remarks & Further Reading:
In my view, the clustering problem is one that has significant applications and still has many areas that people can continue to explore and expand upon to make the problem-solving process easier.
This article certainly cannot fully provide you with all the in-depth knowledge of clustering problems, but I hope that if you are reading this, you can grasp a basic idea of what the clustering problem is, why it exists, and be relatively prepared to approach more advanced materials!
If you are interested in this topic, I will attach some additional references at the end for further reading.
Thank you for reading this far!
Good Luck,
Daves Tran
**Further Reading for Readers:**
James, G., Witten, D., Hastie, T., Tibshirani, R., & Taylor, J. (2023). An Introduction to Statistical Learning. In Springer texts in statistics (pp. 533–535). Springer. https://doi.org/10.1007/978-3-031-38747-0
Nguyen Thi Hop. (2020, February 18). Hierarchical clustering - Data clustering. Viblo; Viblo. https://viblo.asia/p/hierarchical-clustering-phan-cum-du-lieu-maGK7q2elj2
Vu, T. (2017, January 1). Lesson 4: K-means Clustering. Tiep Vu’s Blog. https://machinelearningcoban.com/2017/01/01/kmeans/
Google. (2015). Clustering Algorithms | Clustering in Machine Learning. Google Developers. https://developers.google.com/machine-learning/clustering/clustering-algorithms
Copyright Notice:
Copyright © 2024 Daves Tran